信任区域策略优化 (TRPO)

TRPO 之前的 REINFOCE 算法和 A2C 算法虽然简单、直观，但在实际应用过程中会遇到训练不稳定的情况。具体来说，策略梯度更新参数时很有可能由于步长太长，策略突然震荡，进而影响训练效果。

信任区域策略优化 (Trust Region Policy Optimization, TRPO) 在策略空间中的一个 KL 球 (被称为信任区域, trust region) 内更新策略，在这个区域上更新策略能够使得新策略与原策略较为接近，以得到某种安全保证。TRPO 算法在 2015 年被提出，它在理论上能够保证策略学习的性能单调增强，并在实际应用中取得了比 REINFOCE 和 Actor-Critic 类算法更好的效果。

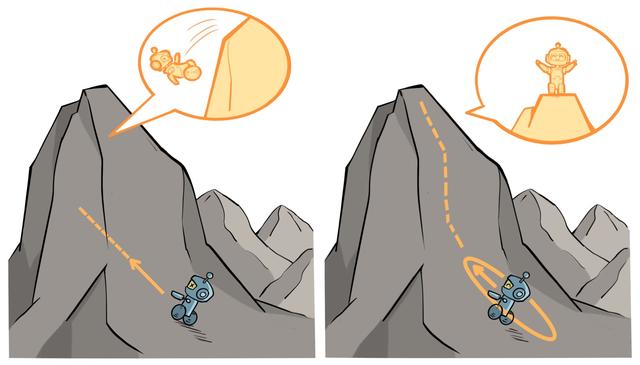
下图直观展示了 TRPO 的原理：

• 左图表示当完全不设置信任区域时，策略的梯度更新可能导致策略的性能骤降
• 右图表示当设置了信任区域时，可以保证每次策略的梯度更新都能来带性能的提升

TRPO 的原理 (图源：《动手学强化学习》)

策略更新目标

TRPO 的策略更新可以表示为：

$$\begin{array}{rl}{\theta }_{k+1}=\arg \underset{\theta }{\max }& \mathcal{L}({\theta }_k,\theta )\\ \text{s.t.}& {\bar{D}}_{KL}({\theta }_k||\theta )\le \delta \end{array}\text{\hspace{1em}(1)}$$

其中 $\mathcal{L}({\theta }_k,\theta )$ 是替代优势 (surrogate advantage), 它使用旧策略 ${\pi }_{{\theta }_k}$ 产生的数据衡量新策略 ${\pi }_{\theta }$ 相对于旧策略的性能：

$$\mathcal{L}({\theta }_k,\theta )={\mathbb{E}}_{s,a\sim {\pi }_{{\theta }_k}}\left[\frac{{\pi }_{\theta }(a|s)}{{\pi }_{{\theta }_k}(a|s)}{A}^{{\pi }_{{\theta }_k}}(s,a)\right]\text{\hspace{1em}(2)}$$

而 ${\bar{D}}_{KL}({\theta }_k||\theta )={\mathbb{E}}_{s\sim {\pi }_{{\theta }_k}}\left[D_{KL}\left({\pi }_{{\theta }_k}(\cdot |s)||{\pi }_{\theta }(\cdot |s)\right)\right]$ 是旧策略所访问的各个状态上，新旧策略的 KL 散度。

近似求解

(1) 给出了理论上的 TRPO 优化目标，但实际上这个优化目标是难以求解的。因此，TRPO 使用了近似的优化目标，并采用了回溯线搜索和共轭梯度算法来求解。

近似优化目标

通过对 (2) 进行泰勒展开可以得到：

$$\begin{array}{rl}\mathcal{L}({\theta }_k,\theta )& \approx g^T(\theta -{\theta }_k)\\ {\bar{D}}_{KL}({\theta }_k||\theta )& \approx \frac{1}{2}(\theta -{\theta }_k{)}^{T}H(\theta -{\theta }_k)\end{array}$$

于是我们得到新的优化问题：

$$\begin{array}{rl}{\theta }_{k+1}=\arg \underset{\theta }{\max }& g^T(\theta -{\theta }_k)\\ \text{s.t.}& \frac{1}{2}(\theta -{\theta }_k{)}^{T}H(\theta -{\theta }_k)\le \delta \end{array}$$

通过拉格朗日对偶法可以得到其解析解：

$${\theta }_{k+1}={\theta }_k+\sqrt{\frac{2\delta }{g^T{H}^{-1}g}}{H}^{-1}g\text{\hspace{1em}(3)}$$

回溯线搜索

由于泰勒展开式引入的近似误差，(3) 可能无法满足 KL 约束，或者实际上提高了替代优势。因此，TRPO 对上述更新规则添加了回溯线搜索 (backtracking line search)。新的更新规则为：

$${\theta }_{k+1}={\theta }_k+{\alpha }^j\sqrt{\frac{2\delta }{g^T{H}^{-1}g}}{H}^{-1}g\text{\hspace{1em}(4)}$$

其中 $\alpha \in (0,1)$ 是回溯系数，而 $j$ 满足：

• ${\pi }_{{\theta }_{k+1}}$ 满足 KL 约束
• 替代优势为正
• 在满足以上条件的非负整数中最小

共轭梯度算法

计算并存储矩阵的逆 $H^{-1}$ 需要非常高的开销，尤其是当处理具有数百万参数的神经网络策略时。TRPO 使用共轭梯度算法 (conjugate gradient) 回避了这个问题，其核心思想是直接计算 $x=H^{-1}g$。

假设满足 KL 距离约束的参数更新时的最大步长为 $\beta$，那么根据 KL 约束有 $0.5(\beta x{)}^{T}H(\beta x)=\delta$，即 $\beta =\sqrt{\frac{2\delta }{x^{T}Hx}}$。因此，参数更新方式 (4) 可以写成：

$${\theta }_{k+1}={\theta }_k+x\sqrt{\frac{2\delta }{x^{T}Hx}}$$

于是我们只需要求解 $x=H^{-1}g$ 即可。可以使用共轭梯度法求解 $Hx=g$ :

1. 初始化 $r_0=g-H{x}_0,p_0=r_0,x_0=0$
2. for $k=0\to N$ do :
   1. ${\alpha }_k=\frac{r_k^T{r}_k}{p_k^{T}H{p}_k}$
   2. $x_{k+1}=x_k+{\alpha }_k{p}_k$
   3. $r_{k+1}=r_k-{\alpha }_{k}H{p}_k$
   4. 如果 $r_k^T{r}_{k+1}$ 非常小，则退出循环
   5. ${\beta }_k=\frac{r_{k+1}^T{r}_{k+1}}{r_k^T{r}_k}$
   6. $p_{k+1}=r_{k+1}+{\beta }_k{p}_k$
3. end for
4. 输出 $x_{N+1}$

在计算 ${\alpha }_k$ 和 $r_{k+1}$ 时，为了避免计算和存储 Hessain 矩阵 $H$，可以使用以下式子，只计算 $Hx$ 向量。对于任意向量 $v$ 有：

$$Hv={\nabla }_{\theta }\left({\left({\nabla }_{\theta }\left({\bar{D}}_{KL}({\theta }_k||\theta )\right)\right)}^T\right)v={\nabla }_{\theta }\left({\left({\nabla }_{\theta }\left({\bar{D}}_{KL}({\theta }_k||\theta )\right)\right)}^{T}v\right)$$

即对梯度和乘法进行换序，先用梯度和向量 $v$ 点乘后再对结果求梯度。

伪代码

TRPO 伪代码 (图源: OpenAI Spinning Up)