时序差分

时序差分 (Temporal Difference, TD) 是强化学习中的一个重要概念，常见于 “TD 算法”、“TD 误差”、“TD 目标” 等名词中。

TD 目标

这里引用《深度强化学习》中的一个例子：

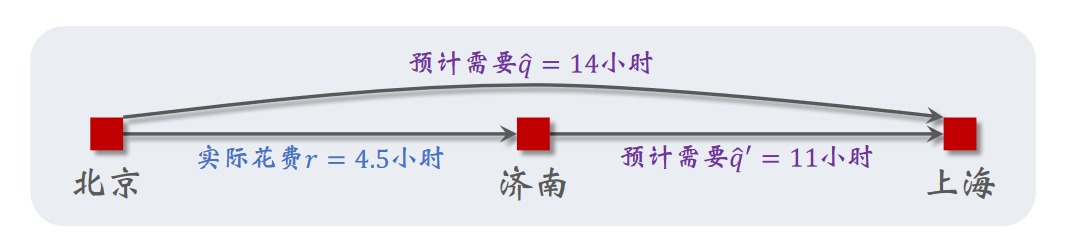
假设模型 (通过某种初始化) 估计从北京到上海一共需要 $\hat{q}=14$ 小时，从济南到上海估计需要 ${\hat{q}}^{\prime }=11$ 小时。智能体实际上花费了 $r=4.5$ 小时从北京到济南。即使智能体没有继续从济南到上海，这一信息也能用于模型的更新。模型对北京到上海的预计总用时可以被更新为 $\hat{y}=r+{\hat{q}}^{\prime }=15.5$ 小时。

这里 $\hat{y}$ 被称为 TD 目标 (TD target)，它比最初的预测 $\hat{q}$ 更加可靠。它被形式化地定义为：

$$\hat{y}=r_t+\gamma \cdot Q(s_{t+1},a_{t+1})$$

TD 误差和 TD 损失

我们可以使用 $\hat{y}$ 对模型做修正。假设模型使用 $w$ 参数化，最初的估计值记为 $\hat{q}=Q(\text{北京},\text{上海};w)$，使用 TD 损失 (TD loss) 作为损失函数：

$$L(w)=\frac{1}{2}{\left[Q(\text{北京},\text{上海};w)-\hat{y}\right]}^2$$

$\hat{y}$ 实际上是 $w$ 的函数，但是我们不会让它参与梯度计算

计算损失函数的梯度得到

$${\nabla }_{w}L(w)=\delta \cdot {\nabla }_{w}Q(\text{北京},\text{上海};w)$$

其中 $\delta =\hat{q}-\hat{y}$ 称为 TD 误差 (TD error)。我们可以用 TD 误差来对神经网络进行更新：

$$w\leftarrow w-a\cdot \delta \cdot {\nabla }_{w}Q(\text{北京},\text{上海};w)$$

这样的学习方式被称为 TD 学习 (TD learning) 或者 TD 算法。

自举与蒙特卡洛

在训练模型时，如果将一个 episode 进行到底，观察所有奖励并进行网络更新 (即在前面的例子中完整地从北京走到上海) ，这种方法被称为蒙特卡洛 (Monte Carlo) 方法，即完整地计算回报 $U_t$，用它去近似它的期望 $Q_{\pi }(s_t,a_t)$。蒙特卡洛方法的好处是无偏性；坏处是其随机性高，方差大，收敛较慢。

而 TD 方法是自举 (bootstrapping) 方法，即使用模型的估计值来更新自身。TD 方法的好处是随机性只来自 $s_t,a_t$, 方差小，收敛较快；坏处是有偏差，因为模型自身的估计可能有偏差。

多步 TD

上面的 TD 目标只使用一个奖励，这样得到的 $\hat{y}$ 是单步 TD 目标。多步 TD 目标 (multi-step TD target) 使用多个奖励，可以视作是单步 TD 目标的推广。

假设 episode 长度为 $n$, 分别写出 $t,t+m$ 时刻的折扣回报：

$$\begin{array}{rl}{U}_t=& r_t+\gamma r_{t+1}+{\gamma }^2{r}_{t+2}+\cdots +{\gamma }^{n-t}{r}_n\\ U_{t+m}=& r_{t+m}+\gamma r_{t+m+1}+{\gamma }^2{r}_{t+m+2}+\cdots +{\gamma }^{n-t}{r}_n\end{array}$$

于是有

$$U_t=\left(\sum _{i=0}^{m-1}{\gamma }^i{r}_{t+i}\right)+{\gamma }^m{U}_{t+m}$$

等式两边关于 $s_{t+1},a_{t+1},...,s_{t+m},a_{t+m}$ 取期望得到

$$Q_{\pi }(s_t,a_t)=\mathbb{E}\left[\left(\sum _{i=0}^{m-1}{\gamma }^i{r}_{t+i}\right)+{\gamma }^m{Q}_{\pi }(s_{t+m},a_{t+m})|s_t,a_t\right]$$

于是得到 m 步 TD 目标 (m-step TD target)：

$$\hat{y}=\left(\sum _{i=0}^{m-1}{\gamma }^i{r}_{t+i}\right)+{\gamma }^{m}Q(s_{t+m},a_{t+m})$$

多步 TD 目标介于蒙特卡洛和自举之间，如果 $m$ 调整得当，可以在方差和偏差之间取得较好的平衡。